[러너게인 블로그] Lecture 11(1). 행렬공간

학습 내용

1. 행렬 공간의 의미
2. 선형대수와 미분방정식의 관계
3. 

 

 

1. 행렬 공간의 의미

---

여태껏 나타낸 열벡터를 그냥 행렬로 나타낸것이다. 

예를들어, [1, 3, 4]T 라는 열벡터가 있으면, 이것은 3차원 공간상의 한 점을 나타내는 벡터엿는데, 

아래와 같이 3x3 행렬이 있으면, 9차원 공간상의 한 점을 나태내는 벡터라고 생각하면 된다. 

 

 

3x3 행렬의 기저들(9개)

 

 

---

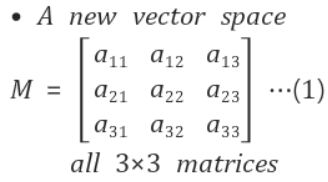
1. 대칭행렬

대칭행렬의 기저

2. 상삼각행렬

상삼각행렬의 기저

3. 대각행렬(1 교집합 2)

-> 대각선에 있는 원소만 남기고 싶은데, 그러면 앞서 1번과 2번의 교집합을 구하면 되는 부분이다

---

(1 합집합 2) = 전체 9x9행렬

 

 

정리

 

 

 

 

 

2. 선형대수와 미분방정식의 관계

---

위와같은 미분방정식이 있으면, 

해는, 

cosX, sinX, e^ix다. 

얘네들은 다시말해 식 12의 영공간(Null Space)을 나타내는 애들이다.

cosX, sinX로만 완전해를 표현해보면

cosX와 sinX의 선형결합으로 식 12의 solution space 즉, Null Space를 나타낼 수 있다. 

즉, cosX와 sinX는 식 12의 Null space를 span 할 수 있는 기저(basis)다. 

 

---

출처

 

[Linear Algebra] Lecture 11-(1) 행렬 공간(Matrix Spaces)