학습 내용
1. Hough Transform Line Fitting
2. Hough Transform Circle
3. Hough Transform Circle C++ 코드구현
1. Hough Transform Line Fitting

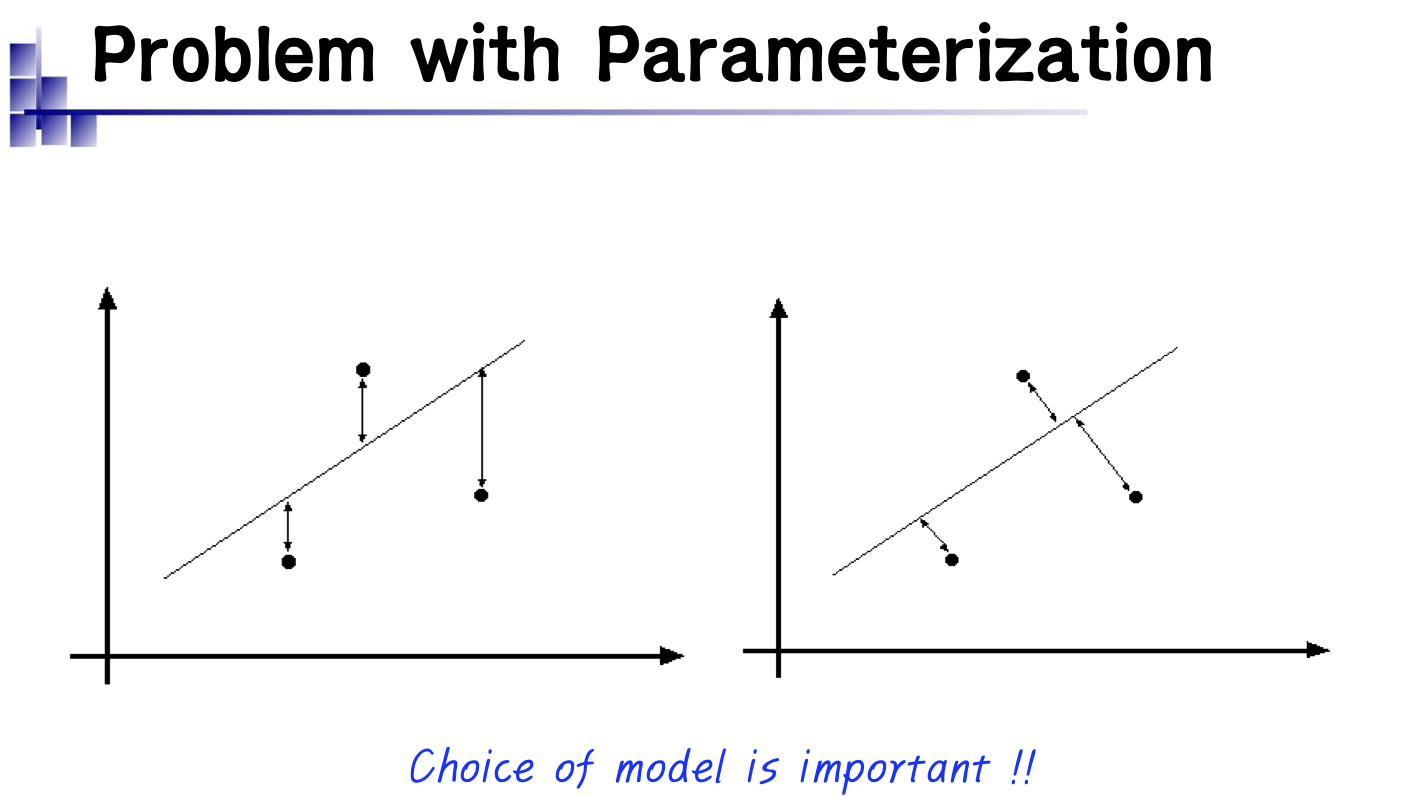
- E는 편차 제곱의 평균. E가 최소가 되게 하는 m과 c를 찾아라!
→ 편미분하여 극소인 점을 찾는것!
- Modeling(=Parameterization)을 y=mx+c로 했다.




2. Hough Transform Circle

- x-y 영역(Image Space)의 한 직선을 rho-theta 영역(Hough Space)으로 옮기면, 한 점이 된다.
- 점 하나 찍으면, Voting(투표) 했다고 말한다.
- Image Space에서 가장 많이 밀집되어 있는 점(가장 많이 voting된 점)이 Image Space에서 직선일 확률이 가장 높다.

- 원을 찾기 위해서 parameterization을 (x-a)^2+(y-b)^2=r^2으로 했다.
- 여기서, r을 알고있다고 하면, 미지수는 a,b이므로, hough space는 a,b점들, 즉, 원의 중심들의 값이 voting된다.
• x-y좌표계에서의 점들이 있다. A(xi, yi)라는 점을 예시로 들면, A점을 지나는 원들은 무수히 많다.
• 그 원들의 중심점을 (a,b)라 하면, a-b좌표계에 점을 찍을 경우, 똑같이 ‘원’이 그려진다.
• 즉, x-y좌표계에서의 한 원은 a-b좌표계에서 한 점으로 대응되는 것이다.
• 즉, x-y좌표계에서의 한 점이 a-b좌표계에서 한 원으로 대응되는 것이다.
• a-b좌표계에서 원들이 가장 많이 겹치는 부분을 주목해야한다.
• 이 점은, x-y좌표계의 점들을 가장 많이 지나는, x-y좌표계 상의 원이다.
• 여기까지, 반지름을 알고 있을때의 방법이고, 아래는 반지름을 모를때, 반지름을 조금씩 키워나가면서 확인하는 방법이다.
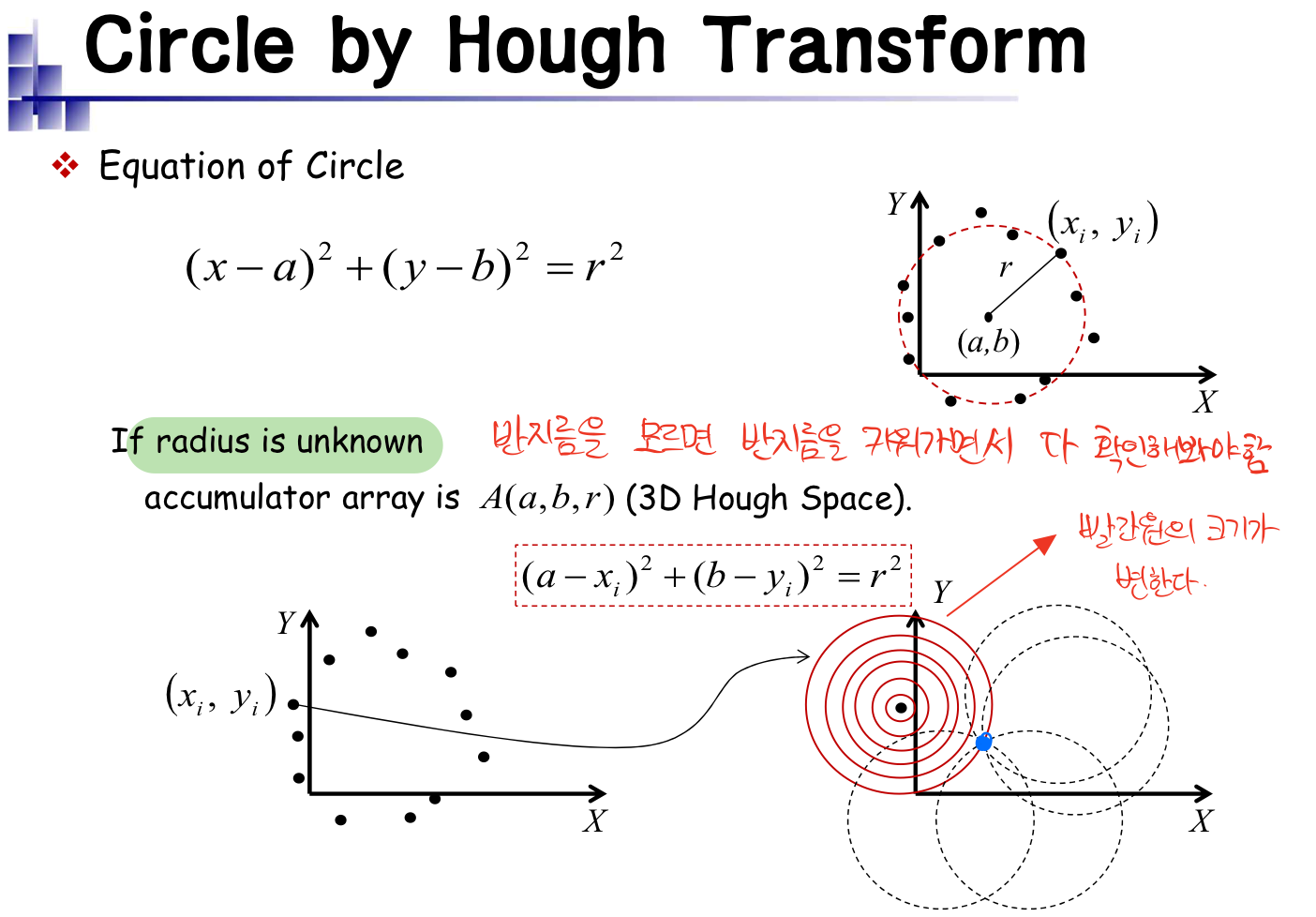
- 반지름을 모르면, r을 키워가면서 a,b를 voting해야한다.

Hough Circle Detector를 코딩으로 구현하려면,
• 일단, (Xi, Yi)들 즉, 엣지 포인트들을 알고 있어야 한다.
• 또, 엣지 포인트 마다 gradient방향을 알고 있어야 한다.
• 반지름을 알고있다면, (Xi, Yi)점을 지나는 원의 중심(a,b)을 위의 수식을 통해 구할 수 있다.
• (a,b)가 산출되면, Accumulator에 하나 축적한다.
• 나중에 Accumulator에서 Local Maxima를 찾으면, 그게 우리가 찾는 원이 된다.
Gradient Information알고있으면, 저렇게 원을 많이 그릴 필요 없다. 금방 찾아낼 수 있다.
Canny Edge를 하면 엣지의 Gradient 방향을 알 수 있다.


3. Hough Transform Circle C++ 코드구현






void Jeong::HoughCircle(const KImageGray& igIn, KImageGray &igOut, KImageGray &igVoting, int R)
{
double dAngleRAD;
Point2d ptCen1, ptCen2;
int nGridCx, nGridCy;
int dx[8] = {1,1,0,-1,-1,-1,0,1};
int dy[8] = {0,1,1,1,0,-1,-1,-1};
KImageGray igEdge(this->_jRow, this->_jCol);
qDebug("%d,%d", igIn.Row(), igIn.Col());
qDebug("check1");
CannyEdgeDetection(igIn, igEdge, 30, 130);
// create voting table
_dSx = 3;
_dSy = 3;
int nNumGridCy = (int)(igIn.Row()/_dSy); // 양자화 → 몇개의 양자가 있을것인가
int nNumGridCx = (int)(igIn.Col()/_dSx); // 양자화
_arVotes.Create(nNumGridCy, nNumGridCx); // row, col 순서
qDebug("check2");
//Cx = k*_dSx
//Cy = k*_dSy
// 반지름 크기 알고있다고 가정하고 한다.
// 반지름 모를때는 3차원 배열을 선언해야함. 내 블로그에 소스 나와있음.
double MaxV = 0;
// Hough Transform Circle
while(!(Edge.empty())){ // Edge는 EdgeInfo* 벡터로, Canny Edge한 결과이다.
//complete circle centers for voting
dAngleRAD = _RADIAN(Edge.back()->_ang); // 라디안 값으로 바꿔줘야함
ptCen1._nx = Edge.back()->_nx - R*cos(dAngleRAD); // 엣지가 바깥으로 향한다고 가정하고 한다. 이게 아니라면 양쪽 다 해줘야한다.
ptCen1._ny = Edge.back()->_ny - R*sin(dAngleRAD);
ptCen2._nx = Edge.back()->_nx + R*cos(dAngleRAD); // 엣지가 안쪽을 향한다고 했을 때
ptCen2._ny = Edge.back()->_ny + R*sin(dAngleRAD); // 엣지가 안쪽을 향한다고 했을 때
Edge.pop_back();
// 엣지가 안쪽을 향한다고 했을 때
if(ptCen1._nx>=0 || ptCen1._ny>=0 || ptCen1._nx <igIn.Col() || ptCen1._ny <igIn.Row()){
nGridCx = (int)(ptCen1._nx/_dSx); // k번째를 구한거다.
nGridCy = (int)(ptCen1._ny/_dSy); // k번째를 구한거다.
// votes to avoid edge noises
for(int i=-5; i<6; i++)
for(int j=-5; j<6; j++){
if(nGridCx+j<0 || nGridCy+i<0 || nGridCx+j>=nNumGridCx || nGridCy+i>=nNumGridCy) continue;
_arVotes[nGridCy+i][nGridCx+j] += 0.7;
if(_arVotes[nGridCy+i][nGridCx+j] > MaxV) MaxV = _arVotes[nGridCy+i][nGridCx+j];
}
_arVotes[nGridCy][nGridCx] += 0.3; // 결국 얘는 1을 더해준꼴
}
// 엣지가 바깥쪽을 향한다고 했을 때
if(ptCen2._nx>=0 || ptCen2._ny<0 || ptCen2._nx <igIn.Col() || ptCen2._ny <igIn.Row()){
nGridCx = (int)(ptCen2._nx/_dSx); // k번째를 구한거다.
nGridCy = (int)(ptCen2._ny/_dSy); // k번째를 구한거다.
// votes to avoid edge noises
for(int i=-5; i<6; i++)
for(int j=-5; j<6; j++){
if(nGridCx+j<0 || nGridCy+i<0 || nGridCx+j>=nNumGridCx || nGridCy+i>=nNumGridCy) continue;
_arVotes[nGridCy+i][nGridCx+j] += 0.7;
if(_arVotes[nGridCy+i][nGridCx+j] > MaxV) MaxV = _arVotes[nGridCy+i][nGridCx+j];
}
_arVotes[nGridCy][nGridCx] += 0.3; // 결국 얘는 1을 더해준꼴
}
}
qDebug("check3");
// Voting 이미지 보기 위해서 다음과 같이 색칠함.
for(int i=0; i<igIn.Row(); i++)
for(int j=0; j<igIn.Col(); j++){
igVoting[i][j] = (int)((_arVotes[(int)(i/_dSy)][(int)(j/_dSx)]) / MaxV * 255);
}
qDebug("check4");
// 8방향 Non-maxima suppression (그냥 제일 voting 많이 된 local maxima를 찾는것)
// 그와중에 Threshold를 넘어야 함.
for(int i=0; i<nNumGridCy; i++) // 행
for(int j=0; j<nNumGridCx; j++){ // 열
int cnt = 0;
if(_arVotes[i][j] < MaxV-0.5) // threshold 걸어줬다. threshold보다 작으면 local maxima여도 의미가 없다.
continue;
for(int k=0; k<8; k++){
int ny = i+dy[k]; // 행
int nx = j+dx[k]; // 열
if(nx<0 || ny<0 || nx>=nNumGridCx || ny>=nNumGridCy)
continue;
if(_arVotes[i][j]<=_arVotes[ny][nx])
break;
cnt++;
if(cnt==8){
CircleCenter.push_back(Point2i((int)(i*_dSy)+(int)(_dSy/2), (int)(j*_dSx)+(int)(_dSx/2)));
}
}
}
// 원 검출한 결과를 표시하기
while(!CircleCenter.empty()){
int a = CircleCenter.back()._nx; // 원의 중심
int b = CircleCenter.back()._ny; // 원의 중심
qDebug("(x, y) = (%d, %d)", a, b);
CircleCenter.pop_back();
for(int y=b-R; y<=b+R; y++)
for(int x=a-R; x<=a+R; x++){
if(x<0 || y<0|| x>=igOut.Col() || y>=igOut.Row())
continue;
if(_SQR(x-a) + _SQR(y-b) <= R*R+50 && _SQR(x-a) + _SQR(y-b) >= R*R-50)
igOut[y][x] = 255;
}
}
}
출처
'Computer Vision' 카테고리의 다른 글
| 16. Generalized Hough Transform (0) | 2021.02.27 |
|---|---|
| 14. Corner Detection(Harris Corner) (0) | 2021.01.22 |
| 13. Canny Edge Detection (Bilinear Interpolation) (0) | 2021.01.22 |
| 12. Edge Detection (Discrete 환경, Noise 환경) (0) | 2021.01.22 |
| 11. Fourier Transform (1) | 2021.01.13 |




댓글